Оригинальный логический вывод структуры, логического фундамента второго закона Ньютона.
Настоящее исследование является свидетельством непреходящей глубины законов Ньютона и творческих подходов к их переосмыслению.
Оно не дает окончательного ответа на вопрос почему закон Ньютона именно таков, но при этом прекрасно освещает как устроена его логическая и концептуальная архитектура.
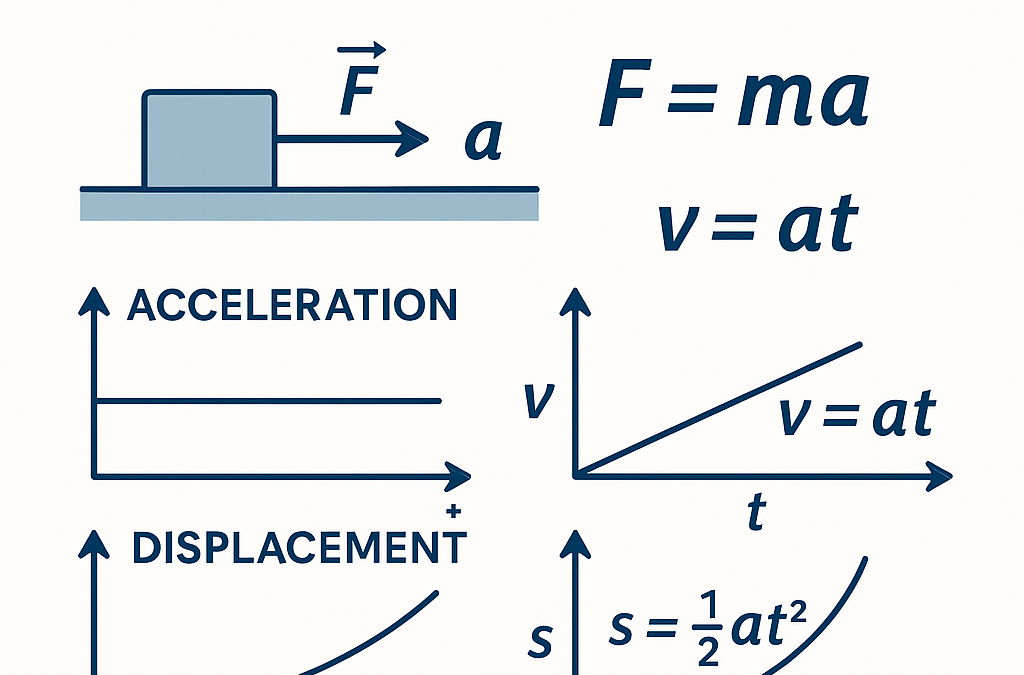
Рассмотрим некоторое тело. Пусть вначале оно покоится. Приложите к нему постоянную силу, например с помощью динамометра. Через короткий промежуток времени Δt тело приобретет скорость Δv.
Перейдем в систему отсчета, в которой тело покоится. И здесь, в соответствии с первым законом Ньютона, за время Δt тело должно набрать ту же скорость Δv. Действительно, пружина динамометра растянута так же, как и прежде (сила постоянна). а законы во всех ннерциальных системах отсчета должны быть одними и теми же.
Теперь снова вернемся в неподвижную систему отсчета. В снлу закона сложеиня скоростей и абсолютности времени в классической механике, имеем, что за время 2Δt тело набирает скорость 2Δv.
Рассуждая аналогично, заключаем, что за время 3Δt тело приобретет скорость 3Δv, а за промежуток времени МΔt — скорость МΔv. А это н означает, что тело движется равноускоренно.
Теперь надо разобрать, почему a = k * (F / m);
где выделенные жирным переменные — векторы
a — ускорение;
k — некоторый постоянный коэффициент, в системе Си единицы измерения подобраны так, что k = 1;
F — сила;
m — масса.
Вопросов о том, что направление векторов ускорения и силы совпадает возникать не должно — мы знаем из опыта, что куда мы тянем, туда — если нет иных сил — тело и ускоряется.
Теперь разберём, почему ускорение будет зависеть от результата деления F / m:
Если сила в 2 Ньютона приложена к телу (материальной точке) в 2 кг, то это то же самое, что 2 (Две) силы по 1 Ньютону приложены к материальной точке массой в 2 кг. Факт очевидный, потому что динамометр, растянутый до силы в 2 Ньютона с одной стороны и 2 других динамометра, растянутых до силы в 1 Ньютон каждый, тянущих 1-й динамометр в противоположную сторону, будут уравновешивать друг друга. Так выстроена шкала силы.
Теперь разделим эту материальную точку массой 2 кг. на 2 материальных точки по 1 кг. И пусть каждый из 2-х динамометров силой по 1 Ньютону будут приложены к своей половине (по 1 кг) материальной точки. Обе материальных точки (каждая половина от исходной) продолжат то же самое движение, потому что каждая из них неотличима от «соседки» и сила к каждой приложена одинаковая. Никаких сил между этими половинами не возникает, потому что они движутся одинаково — есть другая, или её нет. И если даже «связать» их в исходную материальную точку, то тоже ничего не изменится — потому что эта «связь» не будет передавать между половинками точки никакую силу. Таким образом движение материальной точки в 1 кг под действием силы в 1 Ньютон оказывается точно таким же, как движение материальной точки массой 2 кг под действием силы в 2 Ньютона. Этот вывод легко обобщить на любое дробление силы и материальной точки, из чего делаем вывод, что ускорение материальной точки зависит от результата деления F / m.
И нам осталось доказать, что ускорение данной материальной точки массой 1 кг будет пропорционально силе, которая к ней приложена. Тогда мы сможет сделать для произвольных материальных точек вывод о их ускорении пропорционально F / m, потому что вопрос сводится к ускорению материальной точки массой 1 кг под действием силы F / m в силу доказанной только что зависимости ускорения от F / m.
Итак, опираться будем на принцип эквивалентности Эйнштейна, но для классических, а не релятивистских систем. Тогда у нас ускорения складываются при движении ускоренной системе отсчёта, а линейные размеры предметов и интервалы времени в любых системах отсчёта остаются неизменными.
Принцип эквивалентности Эйнштейна нагляден и очевиден для современного человека — внутри космического корабля, свободно падающего в равномерном (всюду одинаковом) поле гравитационного тяготения картина точно такая же, как ели бы на корабль никакой силы не действовало.
Тогда, чтобы понять, как будет двигаться материальная точка массой 1 кг под действием двух приложенных к ней сил F1 и F2 «заменим» силу F1 силой гравитации подходящей по массе планеты. Ведь шкала сил для того и придумана, чтобы действие силы с любой природой, но с данной величиной (векторной) на материальную точку действовало одинаково независимо от природы данной силы. Допустим, под действием силы F1 в «подходящем гравитационном поле» вся наша «падающая» система отсчёта ускоряется с ускорением a1. Внутри этой системы мы вообще никакого ускорения от гравитации не заметим в силу принципа эквивалентности, но «снаружи» вся наша система будет иметь ускорение a1. Теперь приложим к телу внутри этой системы силу F2. Пусть внутри нашей «падающей» системы ускорение нашей материальной точки станет a2. А каким получится общее ускорение нашей материальной точки под действием сил F1 (это гравитация, напоминаю) и F2 с точки зрения неподвижного наблюдателя? По правилам сложения ускорений (нашей «падающей») системы отсчёта с ускорением материальной точки внутри этой системы отсчёта в классической кинематике мы получим векторную сумму a1 + a2.
Таким образом, под действием одновременно двух сил F1 и F2 материальная точка массой 1 кг приобретает ускорение a1 + a2, где каждое из этих ускорений равно тому ускорению, которое получает данная материальная точка под действием только «своей» силы: a1 под действием только F1, a2 под действием только F2.
Имея такое соотношение, мы можем для каждого направления силы свести расчёт ускорения к ускорению от силы величиной в 1 Ньютон. Так как для силы в 2 Ньютона ускорение должно быть в 2 раза больше (это как 2 ускорения от силы в 1 Ньютон) и т.д. Направление ускорения будет то же, что у силы. И очевидно, что все направления в пространстве одинаковы, поэтому для материальной точки массой 1 кг ускорение будет пропорционально силе с одним и тем же коэффициентов в любом направлении:
a = k * F
В силу сказанного ускорение a материальной точки массой 1 кг под действием сил F1 и F2 будет равно:
a = a1 + a2 = k * F1 + k * F2 = k * (F1 + F2)
То есть, ускорение материальной точки массой 1 кг под действием двух сил будет прямо пропорционально векторной сумме этих сил. Вывод очевидно обобщается на любое количество приложенных сил и движение оказывается зависимо только от их векторной суммы.
Таким образом, для материальной точки массой 1 кг мы получили формулу:
a = k * F, где F — векторная сумма (суперпозиция) всех приложенных к данной материальной точке сил.
Переходя к материальной точке любой массы на основе полученной ранее зависимости ускорения исключительно от F / m получаем:
a = k * (F / m)
Переходя в систему Си, где k = 1, получаем:
a = F / m, то есть — второй закон Ньютона.
Что и требовалось доказать.
Научный руководитель Института фундаментальной математики
Дмитрий Леонидович Гуринович
© 1991